What Are The Physics Of "Thick Wall = Cool Smoke"?

[olkofri]

What if... now, hear me out... larger pipes are statistically more likely to have larger bowl diameters, and since the smoker is pulling the same amount of air through a larger airspace, it is traveling slower, resulting in a lower burn temperature?

But remember, once the smoke reaches the draugh hole the channel it travels through gets drastically reduced, and the speed of the smoke is also greatly accelerated. This might be why puffing on the pipe like a cigar scorches your tongue: the hot smoke is traveling too darn fast.

 

[olkofri]

Yes, a significant point. So how does the thickness of a pipe affect--if at all--the smoke and gas once it has been released from the tobacco and/or passed through the ember?

Maybe there's an answer but no satisfaction.

Maybe there's no clear answer, just the continued lore, mystery, dabbling, and speculation of generations of smokers.

No, no. There IS a clear answer. Smoke might twist into mystical shapes but it still follows the laws of physics: it cannot NOT follow them.

The real problem is that when dealing with smoke, including pipe smoke, and air circulations turbulence is involved, and turbulence is a bitch to pinpoint with linear physics: you need to get into chaos physics for that. Good luck with that.

 

[stevecourtright]

In the world of engineering, the perfect heat sink is no heat sink. No matter how good a conductor, a heat sink will hold some heat against the heat producing feature. More wood might affect how hot the bowl feels, but more heat will be kept against the chamber relative to a thinner walled pipe.

 

[rajangan]

But remember, once the smoke reaches the draugh hole the channel it travels through gets drastically reduced, and the speed of the smoke is also greatly accelerated. This might be why puffing on the pipe like a cigar scorches your tongue: the hot smoke is traveling too darn fast.

The diameter of draft holes in pipe stems are pretty much constant, so pipe vs pipe, even if stem smoke speed is a factor, shouldn't matter for the sake of this discussion.

 

[Chasing Embers]

What if... now, hear me out... larger pipes are statistically more likely to have larger bowl diameters, and since the smoker is pulling the same amount of air through a larger airspace, it is traveling slower, resulting in a lower burn temperature?

I've got pipes with basically every size chamber configuration available. Really no difference in flavor or temperature from pipe to pipe, just a longer or shorter smoke duration.

 

[Road To Pines]

But which pipe would subjectively "smoke hotter"? Which would you rather smoke?

Right! So in the space-age ceramic pipe, gas passing through the ember on the inhale will have lost almost none of its heat by the time it reaches your mouth. Ow.

In that case, you'd want the thinnest bowl possible. In the case of an iron pipe, as long as you didn't have to touch it you might want a hefty amount of (heat-conductive) mass where most of the smoke is in contact with it. (It hasn't been established that's the bowl.)

Then there's the question of diminishing returns: how cool can smoke become before it loses pleasant flavor or even condenses and fails to reach the bit?

 

[LBT]

?

Thanks for bringing math into the equation: it does away with all the guessing and the subjectivity.

I'm still having a problem with your conclusion, however:


I'm still failing to see why situation #2 would mean a cooler smoke.

You're welcome

I can appreciate how 2 may be a bit obtuse; for the uninitiated, the inverse relationship with the inequality doesn't help things. So, I'll try to explain and hope that works. Recall:

∂Q-thinner/∂T-thinner > ∂Q-thicker/∂T-thicker

So, assume the heat transfer (∂Q) is equivalent between the two systems. A quick algebraic manipulation later (shown for completeness):

∂Q-thinner/∂T-thinner > ∂Q-thicker/∂T-thicker

∂Q-thinner/∂Q-thicker > ∂T-thinner/∂T-thicker

since ∂Q-thinner = ∂Q-thicker, then ∂Q-thinner/∂Q-thicker = 1

1 > ∂T-thinner/∂T-thicker

or

∂T-thicker > ∂T-thinner

Since these are the same systems, with only the wall thickness different, then that means: ∂T = T-combustion - T-smoke, with ∂T-combustion between the two systems being equivalent. Tn order to preserve the inequality (a larger temp differential with the thicker system vs. thinner system, the T-smoke-thicker must be > T-smoke-thinner. Algebraically:

∂T-thicker > ∂T-thinner

(T-combustion - T-thicker-smoke exit) > (T-combustion - T-thinner-smoke-exit)

- T-thicker-smoke-exit > -T-thinner-smoke-exit

T-thicker-smoke-exit < T-thinner-smoke-exit

I hope that helps, Olkofri!


To the rest, a few comments:

• While smoking characteristics, and briar, and grain, and ember sizes, and everything else vary wildly between one smoke and the next, they were held constant for this analysis, in order to answer the OP's question
• The temperature differential is likely quite small, and I am sure smoking dynamics can overwhelm what difference there is. Therefore, the many views on this subject, based upon the individuals empirical experiences!
• Net/net: For me, over the long run, I take far more pleasure from smoking a pipe, than thermodynamic calculations

Lee

 

[rajangan]

I've got pipes with basically every size chamber configuration available. Really no difference in flavor or temperature from pipe to pipe, just a longer or shorter smoke duration.

And I agree. It's just that some folks in this thread insist that there is a difference between smoke temperature depending on pipe size. In exploring the possibility that they are not imagining things, this is a factor that might actually explain it.

 

[Recon Paul]

I'm not PhD in physics but I play one on the internet.

I'm not an experienced smoker either and I don't have a clever follow up to that.

All that said, heat will always transfer from an area of higher concentration to lower concentration per the 2nd law of thermodynamics. Cooler things absorb heat from hotter things.

Smoke comes from the ember. Therefore it starts out at the same temperature as the ember. It is, after all, a physical remnant of the chemical change of combustion. It travels up the stem into your mouth. As it travels it loses heat to the stem over the short time it travels. This is called the churchwarden effect.

By me.

Since a minute ago.

When I typed that.

Anyway....

At no time does the smoke swirl around the bowl. So the smoke does not transfer heat to the bowl. The ember does. Therefore the structure of the bowl should not affect the heat of the smoke. The blend, the specific temperature of its components, the density of packing, the cadence of smoking, the length and the thickness of the stem, and specific temperature of the material from which it is constructed would all affect the temperature of the smoke when it reaches your mouth.

The thickness of the bowl would only affect the heat reaching your hand.

At least I think so....

 

[Road To Pines]

I've got pipes with basically every size chamber configuration available. Really no difference in flavor or temperature from pipe to pipe, just a longer or shorter smoke duration.

This is my take-away for the evening.

Who knows what tomorrow brings?

 

[Chasing Embers]

Probably my thinnest walled pipe. Smokes cool and barely warm to the touch because of how I smoke.

 

[jpmcwjr]

Yes, in the interest of clarity we need to keep in mind precisely what we're referring to when we say "cooler". I'm inquiring specifically about the temperature of smoke and gas exiting the bit of the pipe.

If there's a differential, it's tiny, or in the mind of the smoker.

Bowl temp is a whole 'other discussion (not that you brought it in.)

 

[Road To Pines]

At no time does the smoke swirl around the bowl. So the smoke does not transfer heat to the bowl.

"Big, if true."

You've voiced my initial take on the matter. I presume, without prejudice, that the heat exchange between smoke and bowl is minimal, especially when intentionally drawn with an inhalation and almost instantly evacuating the chamber.

I also suppose that the width and especially length of the stummel and stem have more to do with any cooling effect, and that the relative masses of smoke itself vs stummel-stem are on such different scales that increasing the amount of material on the pipe would not make any significant difference. Rather, the conductive properties of the materials would make a difference.

And finally, I suppose that in common pipes all of these influences pale in comparison to the effects of smoking technique or tobacco load that burns hot, creates a larger ember, or transfers more heat through moisture.

 

[Road To Pines]

Probably my thinnest walled pipe. Smokes cool and barely warm to the touch because of how I smoke.

View attachment 43603

View attachment 43604

Those two images quieted my mind.

I don't care about the question now! There's just: "How beautiful!"

What a beautifully proportioned, uniquely shaped, invitingly textured pipe.

May all our mental agitations disperse like smoke in vast space. May we take up the opportunity to be struck and stopped by beauty.

 

[olkofri]

The diameter of draft holes in pipe stems are pretty much constant, so pipe vs pipe, even if stem smoke speed is a factor, shouldn't matter for the sake of this discussion.

I concede that the delta in temperature as a result of fluid velocity might be negligible and noticed only by the most sensitive of tongues; yet, a pipe with a larger chamber diameter would push more volume of smoke through the hole and it'd travel faster than it would in a pipe with smaller chamber diameter. The pipe smoking system is nothing but a Venturi tube:

 

[olkofri]

Smoke comes from the ember. Therefore it starts out at the same temperature as the ember. It is, after all, a physical remnant of the chemical change of combustion. It travels up the stem into your mouth. As it travels it loses heat to the stem over the short time it travels. This is called the churchwarden effect.

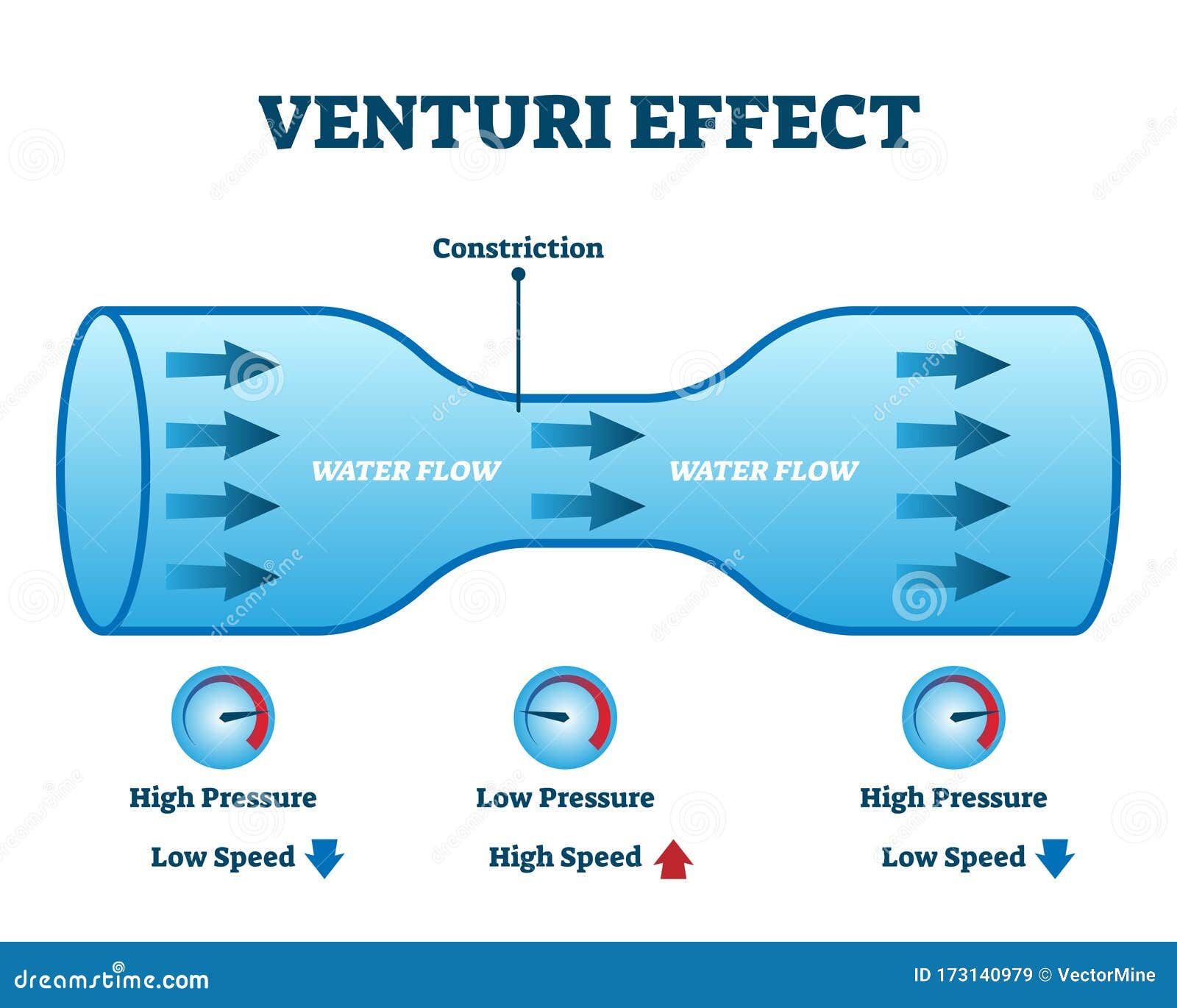
True, but if the smoke is traveling wickedly fast, I venture that its draught-hole-residence-time is not long enough for efficient heat transfer to the stem walls. I've burned the hell out of my tongue with churchwardens.

 

[Road To Pines]

No, no. There IS a clear answer. Smoke might twist into mystical shapes but it still follows the laws of physics: it cannot NOT follow them.

The real problem is that when dealing with smoke, including pipe smoke, and air circulations turbulence is involved, and turbulence is a bitch to pinpoint with linear physics: you need to get into chaos physics for that. Good luck with that.

Yes, thank you. I should have been clearer with my language. There may be no answer for us, at this juncture.

 

[Chasing Embers]

I've burned the hell out of my tongue with churchwardens.

 

[Road To Pines]

I also suppose...

Oh, and also very significant: the duration of contact between smoke/gas and the passageway; and therefore the strength of the draw and the speed of the current through the pipe. (See "venturi effect" elsewhere in this thread.)

 

[olkofri]

Yes, thank you. I should have been clearer with my language. There may be no answer for us, at this juncture.

To further make you go nuts, the answer is actually different for each individual. No: this is not relativism, but science, actually: there are way more factors and variables involved in the actual system than the ideal, simplified system we're discussing here. Mouth anatomy, strength of the draw (which can also vary as per the tension in the muscles of the individual piper, besides smoking technique), environmental factors, differences in pipe construction, turbulence, laminar flow, &c., &c. ... ?

It's easy to see why some smokers might conclude (erroneously) that there's no physics involved. Again, there're plenty of physics there, but it's a chaotic system. All we can do here is approximate, and then have a personal experience, and adjust our variables and technique individually based on what feels comfortable to us. Always follow your tongue. ?